一元一次函数感知器: 如何描述直觉

在很深很深的海底, 住着一个简简单单的生物---小蓝, 他的世界很简单, 去寻找周围能吃到的一种叫做"豆豆"的植物, 并靠此生存.

但是这些"豆豆"在漫长的演化历史中, 通过和小蓝反复的博弈.为了保护自己逐渐进化出了毒性, 毒性的强弱和豆豆的大小有关, 而小蓝也进化出了一个能够检测豆豆大小的器官.

那么问题来了, 小蓝如何根据豆豆的大小判断它有多毒呢?

没错, 他还缺少个思考的的器官, 也就是我们常说的脑子, 但我们又如何描述思考呢? 或者说"认知"呢? 认知以前当然就是一无所知. 这种情况下认知事物的唯一方法就是依靠直觉, 那我们又该如何去描述"直觉"呢?

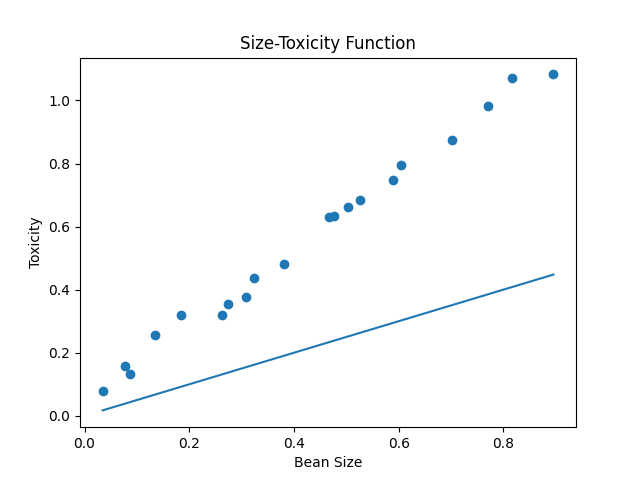
很明显, 是: 函数, 为什么是函数, 仔细想想, 我们本来一直就是用函数认识世界, 豆豆的毒性和大小有关系, 所以这里的直觉自然是一个一元一次函数(y = wx) , 豆豆的大小x是自变量, 毒性y是因变量, 而w是一个确定的参数, 也就是我们常说的直线的"斜率".

一个简单的一元一次函数就可以描述一个直觉, 建立一种思考/认知的模型, 当我们去类比生物神经元的时候, 你就会发现, 用一个一元一次函数描述认知, 可不是乱用的啊, 完全是有被而来, 这实际上就是早在1943年, 由神经学家McCulloch和数学家Pitts在她们合作的论文中, 提出的一种神经元模型(McCulloch-Pitts模型), 这个模型是对生物神经元一种相当简化的模仿.

小蓝靠这个神经元可以存活下来吗? 看的出来随着w取值不同, 这个直觉函数就会产生很多的错误, 这个一元一次直觉函数中的参数w设置多少, 小蓝才能很好的进行预测呢?

也就是说如何从偏离现实的直觉过度到符合现实的认知?

在1958年, 一名叫做Rosenblatt的心理学家在McCulloch-Pitts模型上提出了(Rosenblatt感知器) 模型, 它让神经元有了自己调整权值(w)参数的能力.

Rosenblatt感知器是第一从算法上完整描述的神经元. 在此之后受到它的启发, 工程界, 物理学界, 数学界就开始纷纷投入神经网络的研究, 人工智能也开始蓬勃发展

Rosenblatt感知器是怎么做到"能改"的?

输入通过McCulloch-Pitts模型, 输出一个结果, 用标准答案减去这个结果, 这意味这预测和标准之间的误差, 然后自然是根据这个误差去调整参数, 比如我们让w加上这个误差, 再让结果作为新的w,这样就做到了预测结果过小的时候, 误差为正数, w加上误差之后向大调整, 下次预测的时候结果就提升了, 反过来当预测过大, 误差是负数, w向小调整. 这就是Rosenblatt感知器学习的过程, 通过误差修正参数, 当然在Rosenblatt感知器中误差还要乘以输入的x, 这是为何呢?

我们知道豆豆的大小只能是一个正值, 小于0的豆豆可谓让人匪夷所思, 但是以后我们一定会遇到输入负值的情况, 当输入数据是负数的时候, 你会发现事情正好相反, 预测过大的时候需要增加w, 而不是减少, 而预测过小的时候需要减少w, 而不是增加, 所以我们让输入x乘以误差, 事情就被巧妙的解决了, 当x为正数, 预测过大, 误差为负数乘以x后还是负数, w减少, 预测过小, 误差为正数, 乘以x后还是正数, w增大, 而当x为负数时, 预测过大, 误差为负数, 乘以x后变为正数, w增大, 预测过小, 误差为正数, 乘以x后变为负数, w减小

当然误差除了乘以输入x之外, Rosenblatt感知器模型还让误差乘以一个系数alpha, 比如说0.05, 这意味着我们每次修正的时候幅度降低了20倍, 这个alpha也就是所谓的"学习率", 这又是为何呢?

根据奥卡姆剃刀原理, 我们去除学习率, 会发现调整振幅过大, 容易错过最佳点。

# dataset.py 生成豆豆函数
import numpy as np

def get_beans(counts):
    xs = np.random.rand(counts)
    xs = np.sort(xs)
    ys = [1.2 * x + np.random.rand() / 10 for x in xs]
    return xs, ys

# beans_predict.py
# beans predict 预测豆豆
# McCulloch-pitts 麦克罗克-皮次神经元模型
import dataset
from matplotlib import pyplot as plt

m = 20
xs, ys = dataset.get_beans(m)
print(xs, ys)

# 配置图像 标题,x轴标签,y轴标签
plt.title('Size-Toxicity Function', fontsize=12)  # 设置图像名称
plt.xlabel("Bean Size")  # 设置横坐标的名字
plt.ylabel("Toxicity")  # 设置纵坐标的名字
# 散点图
plt.scatter(xs, ys)

# y = 0.5 * x
# 权值
w = 0.5
# 预测值
y_pre = w * xs
print(y_pre)

# 绘图
plt.plot(xs, y_pre)

plt.show()

# rosenblatt.py
# rosenblatt 罗生布莱特感知器
import dataset
from matplotlib import pyplot as plt

m = 100
xs, ys = dataset.get_beans(m)
print(xs)
print(ys)

# 配置图像
plt.title('Size-Toxicity Function', fontsize=12)  # 设置图像名称
plt.xlabel("Bean Size")  # 设置横坐标的名字
plt.ylabel("Toxicity")  # 设置纵坐标的名字

plt.scatter(xs, ys)

# y = 0.5 * x
w = 0.1

for m in range(m):
    for i in range(m):
        x = xs[i]
        y = ys[i]
        # 预估值
        y_pre = w * x
        # 误差
        e = y - y_pre
        # 震荡系数
        alpha = 0.1
        # 预测w
        w = w + alpha * e * x
        # w = w + alpha * (y-y_pre) * x
        y_pre = w * xs

y_pre = w * xs
plt.plot(xs, y_pre)  # 绘制
plt.show()

print(w)