梯度下降和反向传播: 能改(下)

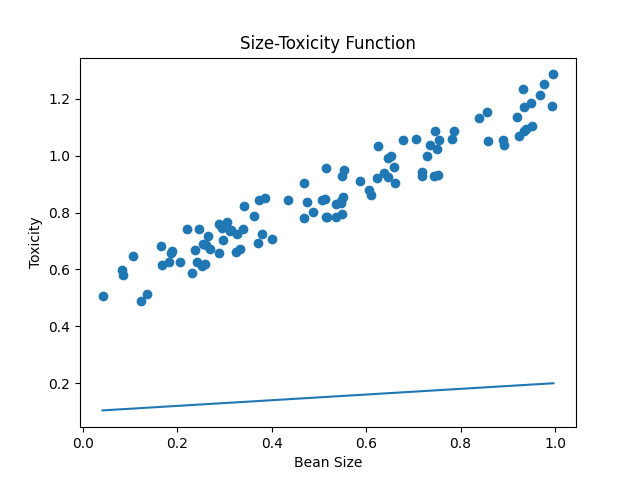
通过上面的学习, 我们已然了解现代神经网络的精髓之一的梯度下降算法, 但是如果仔细观察我们设计的预测函数, 你就会发现, 这是一个非常危险和不完善的模型. 比如在另一片海域里, 豆豆的大小和毒性的关系是豆豆越大毒性越小, 我们发现无论怎样调整w我们都无法得到理想的预测函数, 原因很简单, 我们的预测函数y=wx, 很明显是一个必须经过原点的直线, 换句话说, 这个预测函数直线的自由被限制住了, 只能旋转不能移动. 因为大家很清楚, 一个直线完整的函数应该是y=wx+b, 之前我们为了遵循, "如无必要, 勿曾新知" 的理念, 一直在刻意的避免这个截距参数b. 直到现在, 我们终于避无可避, 是时候增加"新知"了.

截距b的作用大家很清楚, 可以让直线在平面内自由平移, 而斜率w, 它可以让直线自由的旋转. 当我们把直线平移的自由还给它之后, 这两者的结合才能让直线在整个平面内真正自由起来. 我们来看一下加入截距b之后发生的改变, 首先, 我们带入b重新推演一次预测和梯度下降的过程, 当然为了简单我们还是先看单个豆豆样本的情况, y=wx+b是预测函数, 豆豆的大小是x0,毒性是y0,预测是wx0+b, 那么根据方差代价函数得到方差代价是这样的e = (y0-(wx0+b))2 = x02w2+(2x0b-2x0y0)w+(y02+b2-2y0b), 你会发现没有b的时候, 或者b为0的时候, 代价函数是: x02w2+(-2x0y0)w+y02, 那现在既然有了b, 接下来我们就要看这个b取不同的值的时候, 会对代价函数造成怎样的影响, 这里我们需要把代价函数的图像从二维变成三维, 给b留出一个维度, b=0就是我们之前讨论的抛物线, b=0.1, e和w关系还是一个标准的开口向上的抛物线, 因为b的改变只影响这个抛物线的系数, 换句话说, 改变的只是抛物线的具体样子, 而不会让它变成其它形状, 同样的道理, b=0.2, b=0.3 也是, 等等等等, 我们好像已经看出一些眉目了, 这好像是一个曲面, 没错, 我们这里b的取值间隔是0.1, 描绘出来的效果似乎还是不太明显, 当我们把b的取值间隔弄小一点, 知道无限的小下去, 你就会发现, 果真是一个三维空间中的曲面.

那我们该如何看待这个曲面呢? 在有些教程和书籍中, 很多时候为了看着明显, 把它画成了一个鼓鼓的碗状, 其实对于线性回归问题中, 这种豆豆数据形成的代价函数, 实际上并没有那么鼓, 而是一个便便的碗, 扁的几乎看不出来是个碗状, 但是当我们把这个曲面的等高线画出来, 就可以看出这确实也是一个"碗". 很明显这个碗状的最低点, 肯定是问题关键的所在, 我们回忆一下, 在没有b出现的时候, 曲线最低点代表w的取值造成的预测误差最小, 那这个曲面最低点意味着什么呢?

首先想想这个最低点是怎么形成的? 没错, 我们每次取不同的w和b, 都会导致误差e不相同, 这个曲面也就是我们带入b后得到的代价函数的图像, 而他的最低点也就是意味着, 这里的w和b的取值会让预测的误差(代价)最小, 而如果我们能得到这个最低点的w和b值, 放回到预测函数中, 那么此时此刻, 恰如彼时彼刻, 预测也就是最好的, 现在我们的目标就很明确了, 如何在这个曲面上取最低点处的w和b值?

在没有b出现的美好时刻, 也就是说在b=0处, 沿着w的方向切上一刀, 我们知道这将形成一个, 关于e和w的开口向上的抛物线, 然后不断的通过梯度下降算法调整w, 最后到达最低点, 但是你会发现, 此刻曲线的最低点, 却并不是曲面的最低点, 换句话说, b=0的取值并不是最好的, 关于b, 套路其实还是一样的, 我们在这一点如果沿着b的方向给曲面来上一刀, 你会发现, 切口还是一个开口向上的抛物线, 如果是这样的话那就很nice了, 我们在这个抛物线上也向最低点挪动即可, 但果真如此吗?

我们之前已经分析出来e和w的关系是一个抛物线, 现在我们不妨在看一下e和b的关系,
e= (y0-(wx0+b))2,
这是方差代价函数, 要研究b, 那我们围绕b重新整理一下这个式子,
e = b2+(2x0w-2y0)b+(x02w2+y02-2x0yow)
, 当w确定的时候, 也就是我们沿着b的方向切下一刀, 不如当前这个点的w之为wcut, 这个时候代价函数是这样的,
e = b2+(2x0wcut-2y0)b+(x02wcut2+y02-2x0yowcut)
, 也就是把w看作一个确定值的时候, e和b的关系又是一个标准的开口向上的一元二次函数, 所以面对现在这个误差代价函数曲面, 我们还可以换个角度取理解它形成方式, 除了可以向一开始那样认为是e关于w的一元二次函数曲线, 在b取不同的值的时候形成的以外, 也可以认为是e关于b的一元二次函数曲线在每次w取不同的值的时候形成的, 现在我们在b上要做的事情和在w上一毛一样. 不断的调整b, 让它向这个曲线的最低点挪动, 而具体的方法也是一样的, 根据斜率进行下降, 我们完整的来看一下这个过程, 假设一开始我们的w=0.1, b=0.1 , 我们横看此处, 看见的是b确定的时候e和w形成的一个曲线, 根据此处的斜率(导数) 调整w, 大小是斜率(导数)学习率alpha, 方向是根据斜率的正负确定, 我们侧看此处, 看见的是w确定的时候e和b形成的一个曲线, 根据此处的斜率(导数)调整b, 大小是斜率(导数)学习率alpha, 方向根据斜率正负确定, 把这两个方向上的调整运动合成一个合成调整运动, 这样我们就完成了一次调整, 到达下一个点后我们继续横看调整w, 侧看调整b, 当我们反复进行这个过程的时候, 也就逐渐向这个曲面的最低点挪动, 所以说这里同时有w和b的代价函数曲面, 和只有w的代价函数曲线相比, 这个下降过程本质是一样的, 换汤不换药罢了, 或者说只是冲w一味药换成了w和b两味药, 但是有一点我们的代价函数已经是一个曲面了, 这个下降过程如果我们再说是"斜率下降"就不太合适了, 毕竟一个曲面上某点的斜率是个什么东西呢? 是关于w的还是b的呢? 要回答这个问题, 需要发散一下思维, 换一个角度来看这个下降的过程, 我们在代价函数的w和b两个方向上分别求得斜率, 或者说导数, 对于这个有两个自变量的代价函数, 我们先偏向w求导数, 在偏向b求导数, 为了区分只有一个自变量的情况, 为了区分只有一个自变量的情况, 我们把在某一个变量上的导数也称之为"偏导数", 如果我们把对w和对b的偏导数看作向量, 把两个向量合在一起, 形成一个新的合向量, 沿着这个和向量进行下降, 是这个曲面在该点下降最快的方式. 这个合向量在数学里称为"梯度", 到此为止, 你就理解了我们为什么说, 梯度比斜率更广泛的一个概念了. 他是把各个方向上的偏导数(斜率)当作向量合起来形成的一个总向量, 代表着这个点下降最快的方向, 当然在二维曲线中, 因为没有其它方向, 梯度和斜率可以认为是一回事儿, 而为了这个下降算法的名称更具有广泛性, 所以我们一般称之为"梯度下降", 而不是"斜率下降"

# dataset.py
import numpy as np

def get_beans(counts):
    xs = np.random.rand(counts)
    xs = np.sort(xs)
    ys = np.array([(0.7*x+(0.5-np.random.rand())/5+0.5) for x in xs])
    return xs,ys

# cost_function_w.py
import matplotlib.pyplot as plt
import dataset
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

#从数据中获取随机豆豆
m=100
xs,ys = dataset.get_beans(m)

#配置图像
plt.title("Size-Toxicity Function", fontsize=12)
plt.xlabel('Bean Size')
plt.ylabel('Toxicity')

# 豆豆毒性散点图
plt.scatter(xs, ys) 

#预测函数
w=0.1
b=0.1
y_pre = w*xs+b

#预测函数图像
plt.plot(xs,y_pre) 

#显示图像
plt.show()  

#代价函数
ws = np.arange(-1,2,0.1)
bs = np.arange(-2,2,0.1)

#把ws和bs变成一个网格矩阵
#这个网格矩阵的含义可以参考这篇文章:
#https://blog.csdn.net/lllxxq141592654/article/details/81532855
ws,bs = np.meshgrid(ws,bs)
print(ws)#打印出来瞅瞅
print(bs)

es = 0
#因为ws和bs已经变成了网格矩阵了
#一次性带入全部计算，我们需要一个一个的算
for i in range(m):
    y_pre = ws*xs[i]+bs#取出一个样本在网格矩阵上计算，得到一个预测矩阵
    e = (ys[i]-y_pre)**2#标准值减去预测（矩阵）得到方差矩阵
    es += e#把单样本上的方差矩阵不断累加到es上
es = es/m#求平均值，这样es方差矩阵每个点的位置就是对应的ws和bs矩阵每个点位置预测得到的方差

fig = plt.figure()
ax = Axes3D(fig)

ax.set_zlim(0,2)

#plot_surface函数绘制曲面
#cmap='rainbow表示彩虹图（用不同的颜色表示不同值）
ax.plot_surface(ws, bs, es, cmap='rainbow')

#显示图像
plt.show()

# sgd_w_b.py
import dataset
import matplotlib.pyplot as plt
import numpy as np

m = 100
xs, ys = dataset.get_beans(m)

#配置图像
plt.title("Size-toxicity Function", fontsize = 12) #设置图像名称
plt.xlabel("Bean Size") # 设置横坐标名称
plt.ylabel("Toxicity") # 设置纵坐标名称

# 画散点图
plt.scatter(xs, ys)

w = 0.1
b = 0.1
y_pre = w * xs + b

# 画预测直线
plt.plot(xs, y_pre)

# 显示图形
plt.show()

for _ in range(500):
    for i in range(100):
        x = xs[i]
        y = ys[i]
        # a = x^2
        # b = -2xy
        # c = y^2
        # 斜率k = 2aw+b
        # e = 2x^2w + (2xb-2xy) w的导数
        dw = 2 * (x ** 2) * w + (2 * x * b - 2 * x * y)
        # e = 2b+(2xw-2y) b的导数
        db = 2 * b + 2 * x * w - 2 * y
        alpha = 0.1
        w = w - alpha * dw 
        b = b - alpha * db
    plt.clf() # 清空窗口
    plt.scatter(xs, ys)
    y_pre = w * xs + b
    plt.xlim(0, 1)
    plt.ylim(0, 1.2)
    plt.plot(xs, y_pre)
    plt.pause(0.01) # 暂停0.01s