激活函数

通过前面的学习, 我们利用梯度下降算法, 在反复的前向和反向传播的训练下, 已经能够让小蓝从偏离现实的直觉, 自动学习到符合现实的认知, 但是总感觉有点怪怪的, 因为这种精度拟合的方式似乎并不是一个智能体思考的时候常见的模式, 仔细想想我们人在思考的时候, 往往不会产生精确的数值估计, 而更常做的事情是分类, 比如给你一个馒头, 你会说这么大的我能吃饱, 而小一点的我吃不饱, 我们更倾向于把馒头分为能吃饱和吃不饱这两类, 而不会在大脑中构建出所谓的馒头大小和饱腹程度的精确函数曲线, 对一个东西, 简单的贴标签比仔细的计算更符合我们的生物本能, 也就是说, 人类思考问题的方式往往都是离散的分类, 而不是精确的拟合. 对于小蓝也是如此, 若能精确的估算出不同大小的豆豆的毒性, 固然是好事, 但是一般会采用更加干脆的分类, 有毒或者没毒, 假如小蓝本身有一定的抗毒性, 比如最多能抗住0.8的毒性, 只有超过这个毒性的豆豆才会让小蓝中毒, 所以小蓝会更乐意把豆豆分为有毒和无毒两类, 至于具体有多少毒, 那就让小蓝立的科学家们去研究吧. 那这里有我们的数据, 从有毒和无毒的角度来看, 我们的豆豆是这样的(看图), 注意我们的纵坐标不在表示毒性的大小, 而变成了有毒的概率, 1表示有毒, 0表示无毒, 不存在中间值. 所以面对这个两极分化的分类问题, 我们之前的神经元预测函数模型是否还有效呢? 很明显不行, 这个函数的值可以大于1, 也可以小于零, 我们可能跟希望让最后的输出变成这样, 在一元一次函数的输出大于某个阈值的时候固定输出1, 而小于这个阈值的时候固定输出0, 我们可以用一个分段函数很容易实现这一点, 把之前的线性函数的结果, 在丢进一个分段函数中进行二次加工, 而这个新加入的分段函数就是一种所谓的激活函数.

其实我们一开始提到的罗森布拉特感知器中, 也有激活函数, 当时为了不造成困扰, 我们并没有提及, 罗森布拉特感知器把线性函数的计算结果, 放入一个类似的符号函数中进行分类, 也就是说, 到此为止, 我们才算见到完整的罗森布拉特感知器, 当然, 使用这种阶跃函数作为激活函数并不是十分美好, 远的不说, 你看这个大括号看起来就不是个容易处理的家伙, 我们来看看另外一种更好的, 也是常用的s型函数, Logistic函数, 当然, 我们一般采用标准Logistic函数, 也就是取l = 1, k = 1, y0 = 0 , 1/(1+e-y), 可以看出来这个函数的计算结果始终在0到1之间,他的名字逻辑也暗示了这一点, 它很适合做逻辑判断, 也就是分类, 除此之外, 还有一点它很软很圆润, 有的同学或许会说了, 这个圆润的函数看起来好像并没有尖锐的阶跃函数自信啊, 毕竟他有一个渐渐上坡的过程, 如果我们把它应用在我们的分类问题中, 在靠近分界点处他不够果断, 确实, 但是这种软和圆润却是一个极好的特性, 我们知道利用梯度下降算法进行的参数调整, 学习的时候需要对函数进行求导, 也就是求斜率, 我们在加入激活函数后, 同样需要对它进行求导, 相比之下, 如果用类似阶跃函数, 虽然判断的自信满满, 但是在分界点处的导数不好处理而除了分界点, 其它地方的导数总是0无法进行下降, 实际上阶跃函数的导数是一个冲击函数, 在分界出无穷大, 而在其它地方都是零. 这很不利于梯度下降的进行, 所以使用sigmoid这种软软的润润的处处可导, 导数又处处不为零的激活函数是很好的.

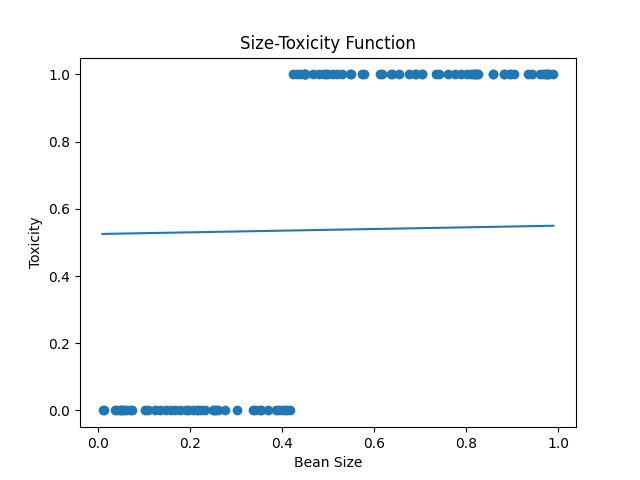
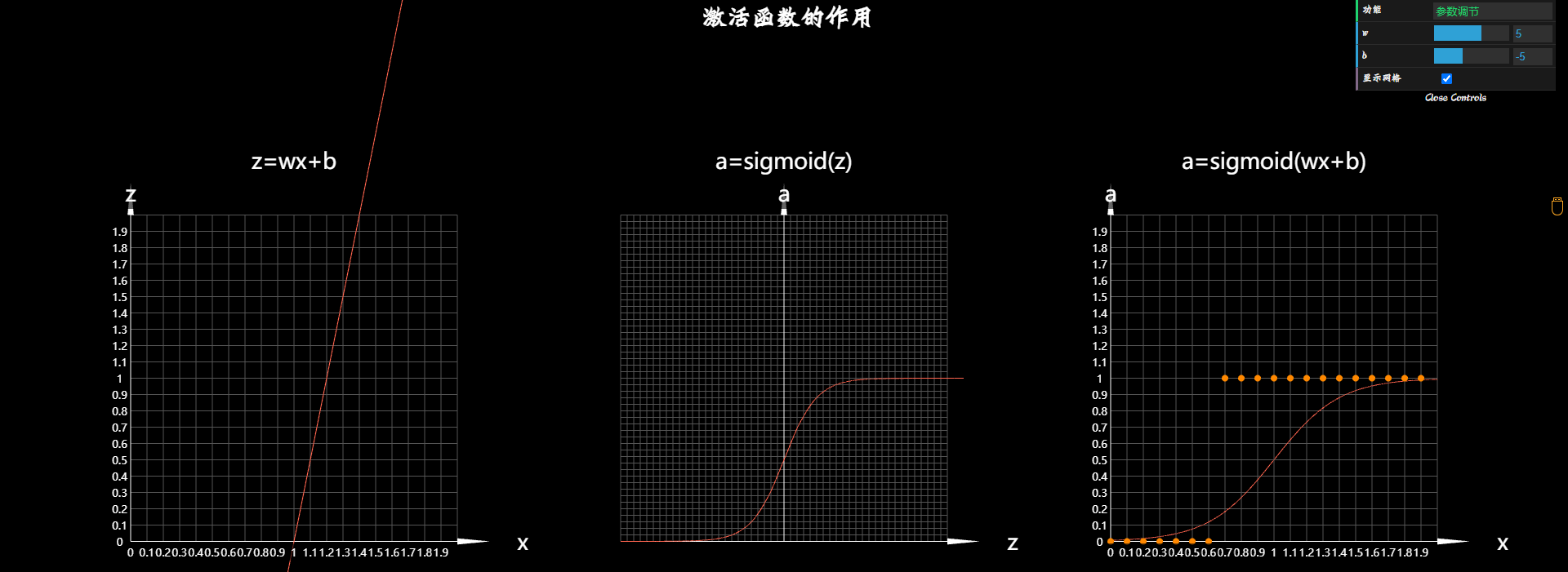
我们来看一下, 把这个圆润的函数, 加入小蓝的神经元作为激活函数之后小蓝现在的想法. 这是环境中的一组豆豆(看图), 有的有毒,有的无毒,z=wx, 这是神经元预测模型的第一部分, 线性函数, 当然线性函数的输出并是不是最终的预测结果, 所以我们用z 表示线性函数的输出, 再把线性函数的结果z作为自变量送入到激活函数中 a = sigmoid(z), 得到a, a才是最后的预测结果. 所以输入x和最终预测输出的a的函数关系是这样的, a = sigmoid(wx+b), 这里对于数学基础比较好的同学, 这三个图像之间的关系, 仔细思考一下就应该很容易的get到, 但是我们还是来简单的讲解下, 首先z和x的关系式, 是一个标准的一元一次函数, x是自变量, z是因变量, 这很简单, 我们改变参数w和b的时候, 这个直线会发生变化, 然后我们把z作为sigmoid的自变量, 输出a, a和z形成一个s形曲线, 那这个时候我们改变w和b, a和z的曲线会发生改变吗? 答案是不是, 因为虽然a的值根据z确定, z的值根据线性函数计算得来的, 但是在形成z和a的曲线的时候, a才不管你的z是怎么来的, 只要你的z等于0, 我的a就等于0.5 只要你的z等于0.2, 我的a就是这么多(a = 0.54), 不会因为你的z是不同的w和b的取值下算出来的, 我就改变啊的值, 所以a和z的曲线就是一个以z等于零的分界线的s型曲线, 不会因为w和b而改变, 那a和x形成的曲线伴随这w和b去不同值的时候, 同样觉得会改变吗? 答案是会, 比如一开始w等于5, b等于-5, 那这时候x要等于1, 计算出来z的z才等于0, a才等于0.5, 所以a和x的图形是这样的, 而如果w等于10, b等于-5, 那么x=0.5, 计算出来的z才等于0, a才等于0.5而且应为w变大了, 随着x的增长, z增长得快, 所以这个s型曲线也就在x方向上被压缩了, 从输入x到输出a, 实际上也就是一个复合函数, 他们通过中间的z产生关系, 那我们可以通过调节w和b来改变, 输入x和最终的输出a的函数图形, 让这个s型曲线可以移动和伸缩. 而调整w和b的方式就是我们之前学习的梯度下降算法, 通过梯度下降算法可以最终让曲线变成这个样子. 非常好的额一个预测。

但此刻对于这个新的预测模型,
z = wx + b
a = sigmoid(z)
a = sigmoid(wx+b)
代价函数:
e = (y-a)^2 = (y - sigmoid(wx+b))^2
我的天哪! 这么复杂的函数, 而且是一个套着一个, 我们该如何对w和b分别求导, 然后进行梯度下降呢? 当然, 最简单和粗暴的方法还是取一个点, 然后利用定义法进行求导, 当然这太麻烦了, 我们又更巧妙的方式, 为了理解上的简单, 我们先不看这个复杂的新模型, 还是用故事最开始的时候, 那个最简单却包罗万象的预测函数模型来琢磨这件事儿. e = (y-wx)^2, 我们曾经用定义法求它的导数, 也曾用求导公式和求导的加法乘法法则求它的导数, 最后我们说关于复合函数的求导法则, 我们日后在说, 那么现在好巧不巧的就是那个当时的日后, 这个函数就是一个复合函数, 我们重新审视一下这个函数,有没有更好的饭食求e对w的导数呢? 没有思路, 再看一眼, 再多看一眼你就会发现这个函数里面是一个一次函数 , 外面是一个二次函数, 也就是说这实际上是一个复合函数,我们把内外两个函数豆明确写出来是这样的, h = y - wx , e = h^2 , 要求这两个函数的导数就十分的easy了, 里层函数的因变量h对自变量w求导是-x, 外层函数因变量e对自变量h求导是2h, 噢! 我的老伙计, 不要去想h到底是什么, 在e = h^2这个函数中它就是一个普通的自变量, 虽然这个自变量h是里层函数的因变量, 但是对于e来说, 他就是我的自变量, 我才不管你是怎么形成的, e是因变量, 这就是一个最简单的一元二次函数, 那么e对w的导数就是直接把这两个导数相乘, 这么神奇吗? 为什么是直接相乘呢? 本课程一般来说不做数学公式的推导和证明. 但是这个复合函数的求导太重要了, 就是它把反向传播和梯度下降这两个现代实际网络的基石优美地结合在了一起, 所以在这里有必要做一个简单的说明, 当然我们并不是在上数学课, 所以不采用微积分教科书中那种严格的, 但是理解起来十分费劲的证明, 我们使用一种更加简单粗暴一点都不严格但是却很好理解的方式, 去简单的理解一下, de/dw = de/dh (dh/dw) = 2h (-x). 我满再用定义法求导的时候, 采用纵坐标的差值除以横坐标的差值, 而且是在差距无限小的时候, 所以在这个莱布尼兹求导符号体系中, 你可以认为上面这个就是因变量的差值, 也可以理解为微分. 而下面这个是自变量的差值, 他俩相除之后就是导数, 而我们目前为止一直在研究一阶导数的问题, 一阶导数具有微分不变性, 所以这个dh可以认为和这个dh是一样的, 所以可以直接约去, 这就是de/dw, 变成了e的差值除以w的差值这不就是e对w的求导吗? 好了, 到这里就可以了, 但是你千万不要和你的微积分老师这么解释问题, 否则任何后果本人概不负责, 以后学习微积分的时候也不要参考我这里的任何讲解, 我们这么讲解, 只是为了然你用最简单的饭食认可复合函数. 通过乘法进行求导的方式, 这种理解方式在微积分的世界里使用范围十分有限, 不过好在我们的课程里的微积分知识还没有跳出这个范围. 那h我们知道等于y-wx, 带入之后就可以计算出e对w的导数 de/dw = zx2w - 2xy, 你说巧不巧, 最后我们之前计算的结果一模一样, 这不是巧不巧的问题, 这就和茴香豆的茴字的四种写法一样, 同一个事情从不同的角度去看待罢了, 不过不同于茴香豆的茴字的写法, 那种迂腐, 我们这里每换一种方法都会让我们的计算和理解更加舒适. 定义法的计算过程很痛苦, 用求导公式加法和乘法的求导法则要轻松一点, 而我们使用复合函数的角度去看待问题的时候, 这个求导的过程就更加的酸爽了. 复合函数就像洋葱, 从内到外一层套着一层, 同样我们对这个复合函数进行求导的方法, 就像剥洋葱, 从外到内一层一层的掀开, 每一层分别把上一层的因变量输出, 作为本层的自变量输入进行求导, 而通过乘法, 导数就像根链条一样, 从洋葱的最外层链到最内层, 最终得到最外层因变量对最内层的自变量的导数, 这就是复合函数的链式法则.

我们知道这种求导方法之后, 对于加入sigmoid激活函数的模型, 代价函数对参数w求导就变得很容易了, 对于这个误差函数, 我们还是先看前向传播的过程,从洋葱的最内层到最外层取构造简单的函数, 再从外到内的去求导, e对a求导是一个简单的二次函数求导问题, e = (y-a)^2 , a对z求导是一个Logistic函数求导问题, a(1-a) , 利用他的求导公式, 我们在编程实验中再来详细说明这件事情. z对w求导是一个简单的一次函数求导问题dz/dw = x, 同样z对b求导也是一个简单的一次函数求导问题dz/db = 1, 再利用复合函数的链式法则把它们乘起来,
de/dw = (de/da) (da/dz) (dz/dw) = -2(y-a)a(1-a)x
, 这样就得到了e对w的导数, 我们在前向传播计算的时候只需要保持好计算的结果a那么把a代入这个式子就很容易计算出具体的结果. 然后利用梯度下降去调整w, 同样的道理, 我们也很容易的求出e对b的导数:
de/db = (de/da) (da/dz) (dz/db) = -2(y-a)a(1-a)1
,实际上, 利用复合函数的链式求导法则, 我们可以很容易计算出更加复杂的预测函数模型的代价函数, 在各个参数上的导数, 比如我们接下来要学习的多层感知器, 或者说多层神经网络. 其本质就是一个嵌套的非常深的复合函数. 当然不仅可以纵向的增加神经元层数, 也可以横向的增加一层神经元的个数. 而利用复合函数求导的链式法则. 把梯度下降和反向传播完美结合后, 不论这个网络有多深有多宽, 我们都可以用同样的套路计算出代价函数在每个神经元上的权值参数的导数, 然后利用梯度下降算法取调整这些参数. 我们会在接下来的课程中, 带你实现一个最简单的多层神经网络. 那时候再来看看具体的操作. 而激活函数除了可以横好地用来分类之外, 也给我们的神经网络注入了灵魂. 我们之前所说的神经元函数的模型, 一直采用的是线性函数, 线性函数说到底能力有限, 对于一个多层的神经网络, 如果每个神经元都是一个线性函数, 那么即使我们很多很多的神经元, 构建出一个复杂的神经网络, 从数学上来说, 她们在一起仍然是一个线性系统. 因为线性函数不论怎么叠加结果都是一个线性函数. 而激活函数是非线性的, 它让我们的神经网络摆脱线性的约束. 开始具备处理越来越复杂问题的能力. 我们将在下一节课中详细说明这个问题. 加入激活函数神经元扩展到多个节点的网络, 这时候也就可以说更一般情况下真正的反向传播算法, 把代价函数在神经网络中反向传播到各个节点, 计算参数对代价函数的影响, 然后调整参数, 正是深度学习的开山鼻祖乔佛里.辛顿和戴维纳姆哈特等人, 在1986年开始在神经网络的研究中, 引入的反向传播算法成为了现代神经网络的基石. 目前深度学习又统治着整个人工智能领域, 而在此之前, 人们对于多层感知器, 深度神经网络一直持有悲观的态度, 正如明斯基和帕波特在反向传播算法发明之前的1961年, 是这么评价的, (尽管(甚至因为!)它具有严重的局限性, 感知器仍然展示了自身的研究价值. 他有很多只得注意的特点: 它的线性性; 它迷人的学习理论; 它清楚地作为一类并行计算范例的简单性. 没有任何理由认为多层感知器仍然具有这些优点. 靠直觉判断多层系统推广是不会有好结果的, 然而, 证明(或否定)这一点仍然是一个很重要的需要研究的问题, 这个现在看起来平平无奇的利用本科一年级就学过的, 复合函数的链式求导法则的反向传播算法, 却是在罗森布拉特感知器发明的27年后才被提出, 正如深度学习领域的另一位巨头人物本吉奥说的那样, 很多看似显而易见的想法, 只有在事后, 才变得显而易见.

# dataset.py
import numpy as np

def get_beans(counts):
    xs = np.random.rand(counts)
    xs = np.sort(xs)
    ys = np.zeros(counts)
    for i in range(counts):
        x = xs[i]
        yi = 0.7 * x + (0.5 - np.random.rand()) / 50 + 0.5
        if yi > 0.8:
            ys[i] = 1
    return xs, ys

# activation.py
# 激活函数

import dataset
from matplotlib import pyplot as plt
import numpy as np

m = 100
xs, ys = dataset.get_beans(m)

# 配置图像
plt.title('Size-Toxicity Function', fontsize=12)  # 设置图像名称
plt.xlabel("Bean Size")  # 设置横坐标的名字
plt.ylabel("Toxicity")  # 设置纵坐标的名字
plt.scatter(xs, ys)

w = 0.1
b = 0.1
z = w * xs + b
a = 1 / (1 + np.exp(-z))

plt.plot(xs, a)
plt.show()

for _ in range(50000):
    for i in range(m):
        x = xs[i]
        y = ys[i]
        # w和b求(偏)导
        z = w * x + b
        a = 1 / (1 + np.exp(-z))
        e = (y - a) ** 2
        deda = -2 * (y - a)
        dadz = a * (1 - a)
        dzdw = x

        dedw = deda * dadz * dzdw

        dzdb = 1

        dedb = deda * dadz * dzdb

        alpha = 0.05

        w = w - alpha * dedw
        b = b - alpha * dedb

    if _ % 100 == 0:
        plt.clf()  # 清空窗口
        plt.scatter(xs, ys)
        z = w * xs + b
        a = 1 / (1 + np.exp(-z))

        plt.xlim(0, 1)
        plt.ylim(0, 1.2)
        plt.plot(xs, a)
        plt.pause(0.01)  # 暂停0.01秒
# y_pre = w * xs
# print(y_pre)
# plt.plot(xs, y_pre)
# plt.show()