高维空间:机器如何面对越来越复杂的问题

如果我们想去判断一个人是否是善于打篮球, 很明显仅仅考虑他的身高特征是不合理的, 虽然这个特征很关键, 但还需要从其它角度去分析, 比如体重, 身体灵活性, 以及是否经常见到凌晨4点钟的太阳等等因素.

同样, 在之前的课程中, 为了让大家更加清晰的了了解神经网络的工作原理, 一直仅仅在用豆豆的大小这个特征去预测它的毒性, 但现实世界往往并非如此简单, 比如豆豆的毒性并不仅和它的大小有关系, 也和它的颜色深浅有关, 当毒性只和大小有关的时候, 我们可以用一个二维的坐标系来描述这个关系, 那此刻加入一个颜色深浅的特征, 该如何用图像描述呢?

很明显我们需要一个3位坐标系,给颜色深浅也指定一个表达维度, 如此我们就可以表示出, 大小和颜色深浅各不相同的豆豆和毒性的关系, 而只有满足某些大小和颜色深浅的豆豆才有毒, 也就是说这些豆豆有毒的概率是1, 其它的是0, 而当输入多了一个颜色深浅数据后, 我们神经元的树突也就需要接受两个输入, 预测函数的线性部分需要从一元一次函数, 变成二元一次函数, "颜色深浅"成为了另一个"元".

很明显, 这是一个有两个自变量, 一个因变量的二元一次函数, 如果我们把这个函数再三维坐标系中画出来, 那么就是一个平面, 正如一元一次函数再二维坐标系是一条直线一样, 这个线性函数的平面经过神经元的第二部分, 非线性激活函数之后, 就被扭曲成了一个s型的曲面, 正如一元一次函数的直线被激活函数扭曲成为一个s型曲线一样. 那么这个曲面就表示当大小和颜色深浅取某个值的时候. 对有毒概率的预测结果, 而当我们找到这个预测曲面上预测值为0.5的点连接在一起, 用地理里的概念来说就是高度为0.5的等高线, 你会发现是一条直线, 这条直线的一边是预测结果大于0.5, 也就是有毒.

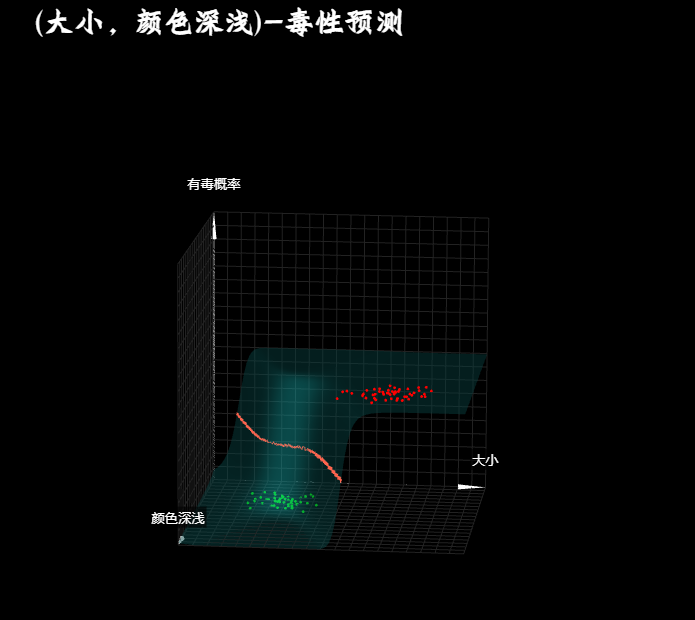
而另一边是预测结果小于0.5, 也就是无毒. 而当我们从上往下看俯视图效果的时候, 这个0.5等高线, 也就是大家可能在很多教程或者书上看到过的类型分割线. 实际上在之前的一元输入(大小), 和有毒概率形成的二维函数中, 也有一个0.5等高线, 只不过在二维空间中国它退化成为了一个点, 你可以称之为"等高点". 而这个等高点同样是两类豆豆的分割"点". 本质上是一样的, 而通过不断的调节权重参数w1,w2以及偏置参数b, 可以让这个预测模型的0.5等高线, 顺利的分割出有毒和无毒两类豆豆. 但是如果环境中豆豆的大小-颜色深浅-和毒性的分布是这样一个情况, 就无能为了.

这就是所谓的线性不可分问题. 我们一开始提到的Rosenblatt感知器便止步于此, 原因我们也说过了, 单个神经元无法做到这一点, 一个二元一次函数再三维空间中形成一个面, 而且必然是平面, 在套上一层sigmoid激活函数后这个面被扭曲为曲面, 然而这个曲面的0.5等高线仍旧是一个直线, 而一个直线并不能分割这种弯曲的边界. 我们可能需要一个曲线来实现这一点, 而解决的办法我们也说过, 那就是再添加隐藏层神经元, 还记得为什么吗?

我们在之前单输入的二维函数中讲过, 从数学上来看, 我们引入多个神经元再通过梯度下降调整, 就可以组合出不同的形状, 在这里, 对于二元输入, 同样, 在引入隐藏层神经元之后, 我们也可以扭曲三维空间中的面. 让它们组合出不同的曲面, 而0.5分割线也就随之被扭曲为一个"曲线". 而通过调整这些神经元的参数, 最终把这个曲面扭曲成想要的样子. 如此也就解决了这种弯曲数据分布的分类问题.

这里, 我个人有一个非常有趣的想法和大家分享一下, 对于之前一元输入的二维预测函数模型, 在加入隐藏层后, 预测曲线被扭曲, 从而得到了两个0.5的等高点, 如果从空间维度的角度做类比, 三维空间中的直线被扭曲后变成曲线, 那么我们似乎可以有趣的把二维空间中的点称之为"直点". 而扭曲之后得到的这两个点称之为二维空间中的"曲点". 当然这是我的命名, 数学中并没有"曲点"的概念. 这里, 给大家留一个可以自行研究的小问题. 如果豆豆的有毒概率和大小, 颜色深浅的分布是一个上图的圈圈, 圈内的有毒而圈外的无毒, 大家想想隐藏层至少需要几个神经元, 才可以把分割线扭曲为一个圆从而实现类型分割?

说到这里, 可以想象, 当问题数据特征越来越多, 也就是说我们采集豆豆的更多特征, 比如除大小, 颜色深浅以外, 在加一个外壳硬度作为输入数据的时候. 我们也可以推而广之, 但这样我们就只能再添加一个维度去描述预测模型的图像, 换句话说我们需要再思维空间作图, 作为三维世界的我们也就心有余而力不足了. 只可意会不可言传. 但是数学作为一种抽象的工具. 却可以很容易的做到这一点. 在数学看来, 这不过就是把输入多加一个维度而已. 而输入数据有多少元素与就是所谓的特征维度. 也叫数据维度, 从一维的大小数据, 到二维的大小-颜色深浅数据, 再到更高维度的数据. 实际上我们把豆豆的特征提取越多, 也就是我们从更多维度去观察问题的时候, 也就能更好的预测它的毒性.

正如当我们从一个人品格, 学识, 性格, 等各种维度去观察他的时候, 才能更好的去理解他, 而不是仅仅从他的身高, 体重和长相, 这些特征或许是他众多特征中对预测最没有用的维度, 到此, 当输入数据的维度越来越多的时候, 我们会发现权重参数也越来越多, 如果一个一个的去写编写它们的函数表达式, 未免有点麻烦和拖沓. 所以我们将在下一节课给大家介绍专门用来处理多维度数据的数学工具, 向量和矩阵, 学会使用向量和矩阵, 在机器学习/神经网络中十分重要. 在下一节课开始, 我们将逐渐走出这些底层的原理分析. 直接采用keras框架来实现神经网络的搭建.

彼时我们不再需要处理前向传播, 也不在需要写反向传播, 甚至梯度下降的细节也会被框架隐藏起来, 但我们唯一逃不脱的就是矩阵和向量的使用, 即使在日后的工作和学习中作为工程人员而不是科研人员化身"调参侠". 我们还是需要熟练的使用矩阵和向量. 然而好消息是矩阵和向量很简单, 从工科的角度来看, 可以说是众多数学分支里最简单的. 而我们课程里用到的相关知识又是最基础和精简的部分.

# dataset.py
import numpy as np

def get_beans(counts):
    xs = np.random.rand(counts,2)*2
    ys = np.zeros(counts)
    for i in range(counts):
        x = xs[i]
        if (x[0]-0.5*x[1]-0.1)>0:
            ys[i] = 1
    return xs,ys

def get_beans2(counts):
    xs = np.random.rand(counts,2)*2
    ys = np.zeros(counts)
    for i in range(counts):
        x = xs[i]
        if (np.power(x[0]-1,2)+np.power(x[1]-0.3,2))<0.5:
            ys[i] = 1

    return xs,ys

# plot_utils.py
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

def show_scatter(xs,y):
    x = xs[:,0]
    z = xs[:,1]
    fig = plt.figure()
    ax = Axes3D(fig)
    ax.scatter(x, z, y)
    plt.show()

def show_surface(x,z,forward_propgation):
    x = np.arange(np.min(x),np.max(x),0.1)
    z = np.arange(np.min(z),np.max(z),0.1)
    x,z = np.meshgrid(x,z)
    y = forward_propgation(x,z)
    fig = plt.figure()
    ax = Axes3D(fig)
    ax.plot_surface(x, z, y, cmap='rainbow')
    plt.show()

def show_scatter_surface(xs,y,forward_propgation):
    x = xs[:,0]
    z = xs[:,1]
    fig = plt.figure()
    ax = Axes3D(fig)
    ax.scatter(x, z, y)

    x = np.arange(np.min(x),np.max(x),0.01)
    z = np.arange(np.min(z),np.max(z),0.01)
    x,z = np.meshgrid(x,z)
    y = forward_propgation(x,z)

    ax.plot_surface(x, z, y, cmap='rainbow')
    plt.show()

# 2_inputs_model.py
import numpy as np
import dataset
import plot_utils

m = 100

xs, ys = dataset.get_beans(m)
print(xs, ys)

plot_utils.show_scatter(xs, ys)

w1 = 0.1
w2 = 0.1
b = 0.1

x1s = xs[:, 0]
x2s = xs[:, 1]

def forward_propgation(x1s, x2s):
    z = w1 * x1s + w2 * x2s + b
    a = 1 / (1 + np.exp(-z))
    return a

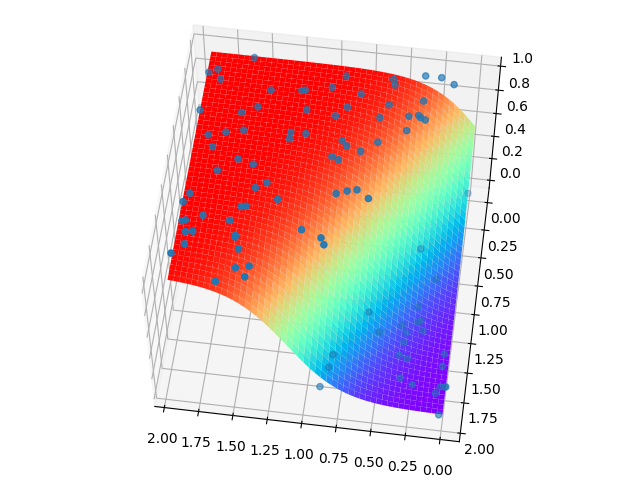
plot_utils.show_scatter_surface(xs, ys, forward_propgation)

for _ in range(500):
    for i in range(m):
        x = xs[i]
        y = ys[i]

        x1 = x[0]
        x2 = x[1]
        a = forward_propgation(x1,x2)

        e = (y - a) ** 2

        deda = -2 * (y - a)
        dadz = a * (1 - a)
        dzdw1 = x1
        dzdw2 = x2
        dzdb = 1

        dedw1 = deda * dadz * dzdw1
        dedw2 = deda * dadz * dzdw2
        dedb = deda * dadz * dzdb

        alpha = 0.01
        w1 = w1 - alpha * dedw1
        w2 = w2 - alpha * dedw2
        b = b - alpha * dedb

plot_utils.show_scatter_surface(xs, ys, forward_propgation)