隐藏层

大自然往往是变幻莫测, 喜怒无常, 在一次地球环境巨变之后, 小蓝所在的海底里的生物也经历了巨大的进化。

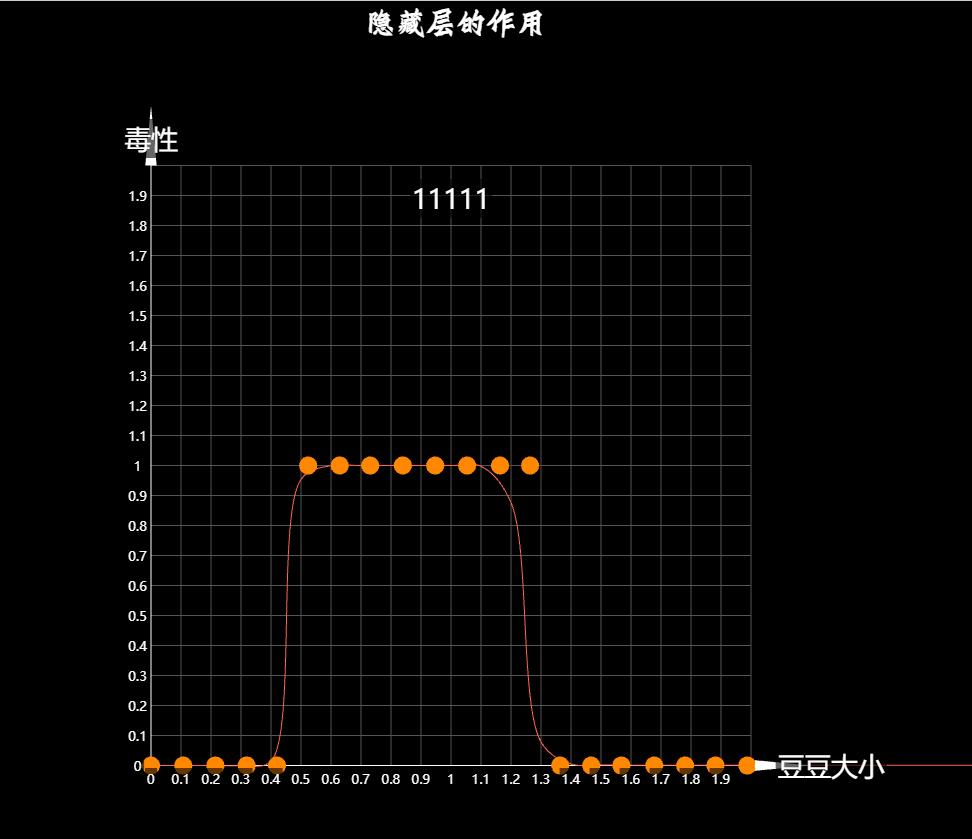
豆豆变得不再是简单的越大或者越小越可能有毒, 而是在某个大小范围内有毒, 而某些范围内没毒, 比如这样(看图)

此时, 不论是不加激活函数的预测模型, 还是加了激活函数的预测模型, 似乎都开始变得无能为力, 因为从数学上来讲, 这些函数再任意范围内的单调性是一样的, 要么处处都是单调增, 那么处处单调减, 而新的豆豆的毒性却变得忽大忽小, 要能预测它们, 只能靠一些不那么单调的函数, 那么如何让预测模型能够产生这种山丘一样的曲线呢?

是时候, 让神经元形成一个网络了, 我们唯一做的事情就是多添加了两个神经元, 并把输入分别送入这两个神经元进行计算, 再把计算的结果送入到第三个神经元计算, 最后输出。

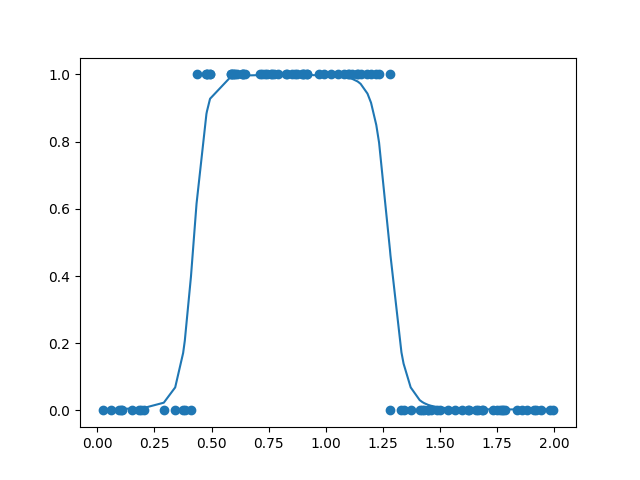
为什么这样呢, 其实很简单, 对于第一个神经元先通过线性函数计算, 在通过激活函数得到最终输出, 而利用梯度下降算法, 最终的输出一定可以被调节成现在这个样子, 第二个神经元也同样, 最终被调节成这个样子, 把这两个神经元的最终输出作为第三个神经元的输入, 先通过第三个神经元的线性函数计算, 乘以权值后变成这个样子, 求和之后是这样, 这时候我们发现这个神经元的线性运算结果, 已然是一个有起伏的不单调曲线了, 在通过激活函数, 并通过梯度下降算法把最终的输出调节成这样, 这就是我们想要的结果, 也就是说, 把输入分为两部分, 然后分别对两个部分进行调节, 然后再送入最后一个神经元, 让整体神经网络形成一个单调性不唯一的更多变函数.从而具备了解决更加复杂问题的能力.

当然, 在这里由于每个神经元里都有一个偏置项b, 也就是线性函数的截距, 一般认为这是大家默认的共识, 所以为了在画网络结构图的时候不那么拖沓, 大家一般都会直接省略这些b, 然我们的网络结构图更加精简, 这就是数学上的解释, 很无趣对吧? 当然, 这里还有一个解释, 虽然其严谨性并不那么好, 但似乎更加有趣, 我们添加一个神经元后, 相当于增加了一个抽象的维度, 把输入放进不同的维度中, 每个维度通过不断的调整权重并进行激活, 从而产生对输入的不同理解, 最后再把这些抽象维度中的输出合并降维, 得到输出.

这个输入数据由于在多个抽象维度中, 被产生不同的解读, 从而让输出的到了更多可能, 同样, 当环境中豆豆的毒性发生更多可能的时候, 我们同样可以采用类似的方法, 通过增加对输入更多的抽象维度, 产生更多的解读而实现更加复杂的分类效果, 而中间这些新添加的神经元节点也称为"隐藏层". 可以看出来, 正是"隐藏层"的存在, 才让神经网络能够在复杂情况下仍旧working, 显而易见的是隐藏层神经元的数量越多, 就可以产生复杂的组合, 解决越复杂的问题, 当然计算量也随之越来越大.

我们已经横向的在神经网络上增加了神经元, 形成了一层隐藏层, 而在之后的课程中, 我们会纵向的不断的添加神经元, 产生更深的隐藏层, 输入通过这些隐藏层, 被一层一层的不断的抽象和理解, 提取出微妙的特征, 从而让神经网络变得更加强大和智能. 而这些隐藏层也就是神经网络为什么working的本质了. 当我们建立一个复杂程度恰当的神经网络, 经过充分的训练后, 网络中各个神经元的参数被调节称为不同值, 这些功能单一的神经元联结组合出来的整体, 就可以近似出一个相当复杂的函数, 可能是这样, 最终变成什么样, 则是根据我们采集的训练数据决定.

我们采集的训练数据越充足, 那么最后训练得到的模型也就能越好的去预测新的问题, 因为越充足的训练数据, 就在越大程度上蕴藏了问题的规律特征, 新的问题数据也就越难以逃脱这些规律的约束,所以我们总说机器学习神经网络的根基是海量的数据, 一个训练之后拟合适当的模型, 进而在遇到新的问题数据的时候也能大概率产生正确的预测., 我们把这个现象称之为模型的"泛化", 模型的"泛化"能力也就是神经网络追求的核心问题. 我们经常听到的"深度学习"其中"深度"二字其实并没有什么特别的奥义, 只是指一个神经网络中纵向的隐藏层比较多, 换句话说, 很深.

我们一般把隐藏层超过3层的网络就称之为"深度神经网络", 这也就是深度学习中广受诟病的地方, 隐藏层的神经元理解什么, 提取什么豆太过微妙, 虽然我们对大致的结果也有所把握, 但却很难用精确的数学去进行描述, 我们能做的也只有设计一个网络, 送入数据, 然后充分的训练, 如果得到的预测效果好, 我们就会说"它起作用了", 如果不好,那也只能说"搞错了, 调调参数, 再来一遍".

所以很多人戏称深度学习是"炼丹", 确实, 道士把原材料(数据) 放入八卦炉(神经网络), 开火炼丹(训练) 最后得到的仙丹可能让人长生不老, 也可能让人一命呜呼. 炼丹过程中八卦炉里发生的微妙事情, 道士也是不得而知的, 虽然是他设计了炼丹一切.

# dataset.py
import numpy as np

def get_beans(counts):
    xs = np.random.rand(counts) * 2
    xs = np.sort(xs)
    ys = np.zeros(counts)
    for i in range(counts):
        x = xs[i]
        yi = 0.7 * x + (0.5 - np.random.rand()) / 50 + 0.5
        if yi > 0.8 and yi < 1.4:
            ys[i] = 1

    return xs, ys

# one_hiden_layer_net.py
# 隐藏层
import numpy as np
import dataset
from matplotlib import pyplot as plt

m = 100
xs, ys = dataset.get_beans(m)

# 配置图像
plt.title('Size-Toxicity Function', fontsize=12)  # 设置图像名称
plt.xlabel("Bean Size")  # 设置横坐标的名字
plt.ylabel("Toxicity")  # 设置纵坐标的名字

plt.scatter(xs, ys)
# 第一层
# 第一个神经元
w11_1 = np.random.rand()
b1_1 = np.random.rand()

# 第二个神经元
w12_1 = np.random.rand()
b2_1 = np.random.rand()

# 第二层
w11_2 = np.random.rand()
w21_2 = np.random.rand()
b1_2 = np.random.rand()

# 激活函数
def sigmoid(X):
    return 1 / (1 + np.exp(-X))

# 前向传播
def forward_propgation(X):
    z1_1 = w11_1 * X + b1_1
    a1_1 = sigmoid(z1_1)

    z2_1 = w12_1 * X + b2_1
    a2_1 = sigmoid(z2_1)

    z1_2 = w11_2 * a1_1 + w21_2 * a2_1 + b1_2
    a1_2 = sigmoid(z1_2)
    return a1_2, z1_2, a2_1, z2_1, a1_1, z1_1

a1_2, z1_2, a2_1, z2_1, a1_1, z1_1 = forward_propgation(xs)
plt.plot(xs, a1_2)
plt.show()

for _ in range(5000):
    for i in range(m):
        x = xs[i]
        y = ys[i]
        # 先来次前向传播
        a1_2, z1_2, a2_1, z2_1, a1_1, z1_1 = forward_propgation(x)

        # 反向传播
        # 误差代价 e
        e = (y - a1_2) ** 2

        deda1_2 = -2 * (y - a1_2)

        da1_2dz1_2 = a1_2 * (1 - a1_2)
        da1_1dz1_1 = a1_1 * (1 - a1_1)
        da2_1dz2_1 = a2_1 * (1 - a2_1)

        dz1_2dw11_2 = a1_1
        dz1_2dw21_2 = a2_1
        dz1_1dw11_1 = x
        dz2_1dw12_1 = x

        dz1_1db1_1 = 1
        dz1_2db1_2 = 1
        dz2_1db2_1 = 1
        dz1_2da1_1 = w11_2
        dz1_2da2_1 = w21_2

        dedw11_2 = deda1_2 * da1_2dz1_2 * dz1_2dw11_2
        dedw21_2 = deda1_2 * da1_2dz1_2 * dz1_2dw21_2
        dedw11_1 = deda1_2 * da1_2dz1_2 * dz1_2da1_1 * da1_1dz1_1 * dz1_1dw11_1
        dedw12_1 = deda1_2 * da1_2dz1_2 * dz1_2da2_1 * da2_1dz2_1 * dz2_1dw12_1

        dedb1_2 = deda1_2 * da1_2dz1_2 * dz1_2db1_2
        dedb1_1 = deda1_2 * da1_2dz1_2 * dz1_2da1_1 * da1_1dz1_1 * dz1_1db1_1
        dedb2_1 = deda1_2 * da1_2dz1_2 * dz1_2da2_1 * da2_1dz2_1 * dz2_1db2_1

        # 梯度下降
        alpha = 0.03
        w11_2 = w11_2 - alpha * dedw11_2
        w21_2 = w21_2 - alpha * dedw21_2
        b1_2 = b1_2 - alpha * dedb1_2

        w12_1 = w12_1 - alpha * dedw12_1
        b2_1 = b2_1 - alpha * dedb2_1

        w11_1 = w11_1 - alpha * dedw11_1
        b1_1 = b1_1 - alpha * dedb1_1

    if _ % 100 == 0:
        plt.clf()  # 清空窗口
        plt.scatter(xs, ys)
        a1_2, z1_2, a2_1, z2_1, a1_1, z1_1 = forward_propgation(xs)
        plt.plot(xs, a1_2)
        plt.pause(0.01)  # 暂停0.01秒